GPS is one of the wonders of the modern age (RIP, LORAN). But while GPS is great for showing your position, it's not so good at showing altitude. Part of the problem is the satellite geometry makes for poor triangulation of elevation. But worse, elevation itself is difficult to define.

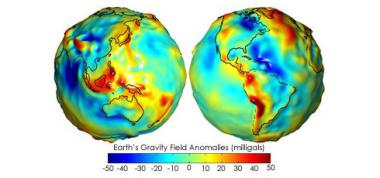
If you're flying a plane, what you care about is how far you are above the ground (AGL). GPS won't tell you that since it doesn't know where the hills are. But GPS can tell you your altitude above sea level (MSL), which you can then compare to a map which shows terrain in terms of MSL.

But where is sea level? Annoyingly, that's locally defined. Naively you'd just measure your distance from the center of the earth. Which is more or less what GPS does in that positions are defined relative to WGS84. The earth's not quite a sphere, so WGS84 is actually a pole-flattened spheroid, the polar distance is 0.335% shorter than the equatorial. GPS calculates your altitude above that spheroid.

But the earth isn't a uniform object, it's lumpy. I don't mean the mountains, but rather the varying density inside the earth causes ripples in the gravimetric field. If you could conceptually flood the earth with enough water to cover all the mountains, the resulting global sea would not be flat.

So good GPS receivers correct the WGS84 spheroid with a Geoid model, a detailed approximation of the lumpiness of earth's gravity. Most folks now use EGM96, which is a harmonic model with 360 coefficients in each direction, resulting in 5MB of constants for correction. There's a new finer-grained geoid just in production now, EGM2008, with 240 megs of constants. These corrections sound like niceties, but they're quite significant. For instance at my house the EGM96 correction is 106 feet. You don't want to fly a plane 106 feet underground.

One last bit of detail: how do we know where the GPS satellites are? Their position is measured and updated regularly from ground stations. But everything in the universe is moving, so what do you measure position relative to? Answer: quasars. Astronomers define the International Celestial Reference Frame relative to the position of 212 quasars. Those quasars are themselves moving, but they're so far away that their apparent motion to us on earth is near zero and so we pretend they're fixed landmarks to reckon against.

I love how GPS combines deep space astronomy, orbital mechanics, gravimetry, geology, and good old fashioned geography and survey work to tell us where we are with some accuracy. And don't forget special and general relativity, too!